
 It turns out that the single most fundamental and pervasive operation for a Knowledge Level (KL) system is lookup by name or other identifying tag string. In a general sense this requires “Content Addressable Memory” (CAM). Because the CAM lookup operation is so pervasive in KL systems, often accounting for well over 50% of CPU time in common operations, an extremely fast algorithm or preferably a hardware implementation is required. Unfortunately standard CPUs provide no hardware support for CAM, which means a software algorithm must serve. Current approaches use hashing schemes, but these generally provide no means to get ‘close’, say if a name is slightly misspelt. Nor do hashes generally help with ‘paths’ and hierarchies which are fundamental to organizing ontological/KL data. If the hash lookup fails, you are essentially back where you started. Finding a solution to this problem is a key first step in implementing a KL system.
It turns out that the single most fundamental and pervasive operation for a Knowledge Level (KL) system is lookup by name or other identifying tag string. In a general sense this requires “Content Addressable Memory” (CAM). Because the CAM lookup operation is so pervasive in KL systems, often accounting for well over 50% of CPU time in common operations, an extremely fast algorithm or preferably a hardware implementation is required. Unfortunately standard CPUs provide no hardware support for CAM, which means a software algorithm must serve. Current approaches use hashing schemes, but these generally provide no means to get ‘close’, say if a name is slightly misspelt. Nor do hashes generally help with ‘paths’ and hierarchies which are fundamental to organizing ontological/KL data. If the hash lookup fails, you are essentially back where you started. Finding a solution to this problem is a key first step in implementing a KL system.
A separate but related problem for any system attempting to ingest multiple structured and unstructured sources into a
unifying ontology is the need to provide
parsers capable of processing each source. Clearly if a system is to be adaptive, these parsers must be created on-the-fly as needed by each source, that is they cannot require a ‘compilation’ in order to support a new source/language. This means that both the parser and the lexical analyzer must be dynamically created and table driven. Current
lexical analyzer generators (e.g.,
LEX) generate C code as output and so require recompilation, making them unsuitable for adaptive KL use. We need a dynamic, flexible, non-compiled, yet blindingly fast lexical analyzer for each of the many interpreted languages that form components in a KL architecture. Finally of course,
Lexical analysis of all human languages (in
UTF-8) must be possible. Most stuff of interest happens first in a language other than English. Any system that ignores this fact is guaranteeing an unacceptable data latency, and probably irrelevant results. Handling these requirements is quite a different matter from implementing a lexical analyzer for simple programming languages.
In this post I want to introduce Mitopia’s
patented solution that simultaneously solves both of these problems, and thus unifies the previously distinct fields of lookup and lexical analysis. This technology is implemented in Mitopia’s Lex package.
All conventional lexical analyzer generators follow the same sequence of three steps to generate the tables necessary to drive lexical analysis. These steps are as follows:
- translate regular expressions into a non-deterministic finite automaton (NFA)
- translate the NFA into a deterministic finite automaton (DFA)
- optimize the DFA (optional)
In an NFA, there may be multiple different transitions from any given state to other states for the same character, and this means that the NFA table cannot be used directly for lexical analysis, it must be converted to a form where for any given state and input character, the resulting state is unique, this is the DFA. The classic algorithm for converting an NFA to the equivalent DFA (the subset construction algorithm) is well known and can be summarized as follows:
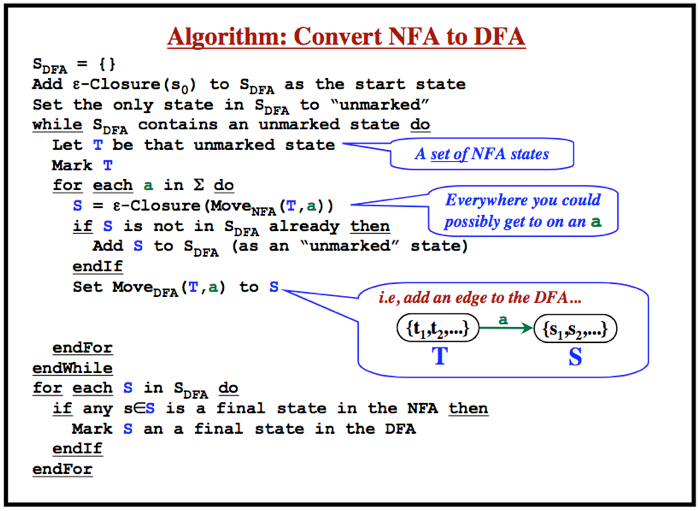 |
|
Figure 1 – Algorithm to Convert an NFA to a DFA
|
In the worst case, there can be an exponential number O(2**N) of sets of states and the DFA can have exponentially many more states than the NFA, but this is rare. There is a trade-off to be made. Backtracking lexical analyzers based on NFAs are possible, and these favor linguistic expressiveness while incurring the possibility of exponentially slow execution time caused by all the backups. DFA implementations minimize asymptotic time complexity for the lexical analyzer, but are somewhat less expressive, and incur the lengthy generation process of converting the NFA to the DFA and the resultant huge size of the DFA for any non-trivial language.
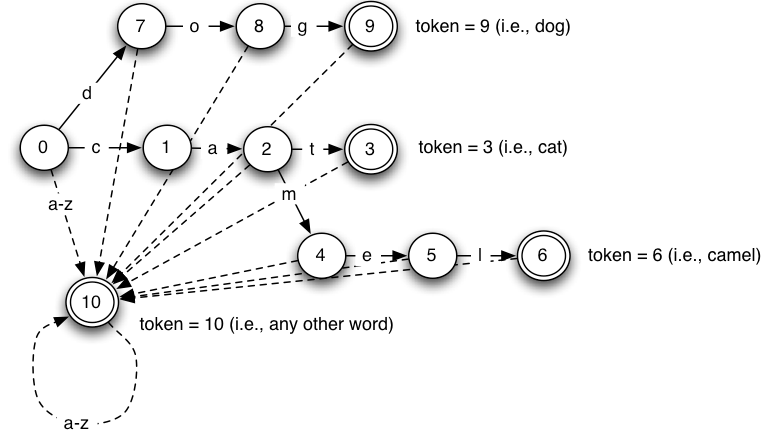 |
| Figure 2 – Example Lexical Analyzer State Transition Diagram |
In most applications a lexical analyzer is responsible for scanning sequentially through a sequence of characters in an input stream and returning a series of numeric language tokens to a parser which may use these tokens to determine what kind of string was encountered. As mentioned earlier, lexical analyzers are implemented as finite-state machines, that is as each character is consumed from the input stream, it causes the lexical analyzer to move from its current state to some new state. Certain states are designated as ‘accepting’ states (double bordered circles in the figure above), and if the lexical analyzer reaches an ‘accepting’ state, and the input stream runs out or the next character is white space (and possibly one of a number of specified delimiter characters), the lexical analyzer returns a token corresponding the the final state to the parser.
If the lexical analyzer is in a non-accepting state and there is no path to another state labelled with the next character in the stream, the lexical analyzer has failed to recognize the input given and returns a failure indication. In the figure above we see a very simple lexical analyzer state diagram that recognizes the three special strings “dog” (token 9), “cat” (token 3), and “camel” (token 6), all other strings of alphabetic characters will result in returning the generic “word” token 10. Note that there are two types of transition lines in the diagram. The solid lines which represent a single ‘catalyst’ character that drives the state from the starting state to the ending state if encountered next in the stream. The dotted lines represent a range of ‘catalyst’ characters that if encountered will drive the state to the final state. In this diagram, all the dotted lines represent the range a-z. Note however that there is ambiguity in this diagram for example if in state 8 the next character is ‘g’, should the new state be 9 (as specified by the solid line), or 10 (as specified by the a-z dotted line)? The example figure above is therefore an NFA, not a DFA. It is easy to see that even for the simple diagram shown, the range transitions represent a vast number of possible paths through the automata which accounts for the massive table expansion when converting from an NFA to a DFA.
Problems with Classical Lexical Analysis
The first problem with classical approaches to auto-generated lexical analyzers relates to execution time tradeoffs. If one chooses the NFA-based approach:
- Execution time to process input is O(s**2 · L) ,where s is the number of NFA states, and L is the length of the input.
- Need O(s**2) time in running ?-closure(T) assuming using an adjacency matrix representation and a constant-time hashing routine with linear-time preprocessing to remove duplicated states.
- Space complexity is O(s**2 · x) using a standard adjacency matrix representation for graphs, where x is the cardinality of the alphabet.
If one chooses the DFA-based approach, running time is linear with the input size, and the space requirement is linear with the size of the DFA but:
- May get O(2**s) DFA states by converting an s-state NFA.
- The converting algorithm may also take O(2**s·x) time in the worst case.
- For typical cases, the execution time is O(s**3).
This tradeoff is generally the reason why high performance real-world compilers opt for carefully hand-crafted recognizers over the use of a formally generated table-driven approach.
A second major shortcoming of most current lexical analyzer generators is that their output is source code which, once generated, must then be pasted into the containing program and compiled in order to create a functioning executable. This rules out the use of such lexical analyzers in dynamic situations such as when the compiler must be generated and then executed on the fly in response to an external specification. This is exactly the situation that Mitopia® faces all the time when mining new source data, in that the parser and lexical analyzer specifications for each distinct source are unique, and may never have been encountered before. The same is true of many other aspects of Mitopia® operation, indeed it is perhaps a fundamental truth, that any system that attempts to be truly data-driven and extensible, rather than pre-determined at compile time, must address and solve this compile-time shortcoming of current lexical analysis and parsing technologies. There is simply no way around it.
Another issue with classical approaches comes up when one attempts to extend the character domain beyond the classical ASCII or English character set. Much of the information in the world is written in languages other than English, and much of that is in non-Latin scripting systems (e.g., Arabic, Chinese, Korean, etc.). The problem of encoding these languages and scripts for computer use has been solved by use of the UTF-8 encoding scheme which allocates from 1 to 6 bytes to encode any given symbol/character in a scripting system. This variable size for each symbol that might be combined in sequences to make up a token (e.g., a word in the language) breaks the classical table-driven approaches, and means they cannot generally be used to interpret languages other than those based on ASCII. Once again, this makes them unsuitable for use with any system that is attempting to process multilingual data through the lexical analyzers. Many other areas of Mitopia® require to do just that.
The Mitopia® Lexical Analyzer Package
Mitopia’s lexical analyzer ‘Lex’ takes a unique approach to addressing the finite state machine problem by splitting the lexical analysis process into two distinct phases, the first of which handles only single catalyst deterministic (DFA) transitions (described by the ‘OneCat’ table), and the second of which only executes if the single catalyst transitions fail to reach an accepting state. In the second phase, if it occurs, the lexical analyzer starts back at the beginning and tries to recognize the word by sequentially scanning an ordered sequence of range transitions. The second range table (referred to as the ‘CatRange’ table) is allowed to be non-deterministic, with all ambiguities being resolved purely by the order in which the range transitions are scanned.
This approach means that Lex is essentially a hybrid approach having two non-overlapping phases, the first being deterministic and used only to recognize reserved words and specialized language tokens, and the second non-deterministic phase being used to recognize the variable content tokens such as identifiers and numbers. This completely eliminates the problem of NFA to DFA conversion and reduces the size and complexity of the state machine table dramatically. The approach is based on the premise that any realistic language has only a very limited number of variable content token types, usually less than 16, whereas it may have a much larger set of reserved word tokens, especially in data-mining situations. Thus by separating the recognition of the two types of token into distinct phases, the state machine complexity caused by the ambiguities between reserved words and variable names goes away.
There are many benefits from taking this patented two-phase approach, the foremost of which is that since the two phases are distinct and described by separate structures (see below), it is possible to design the single transition data structures so that they can be dynamically modified to add new unique strings to the recognizer without adversely impacting recognition of all the existing strings. This creates the possibility that the lexical analyzer can be used independent of a parser as a dynamic dictionary lookup capability, and indeed this forms the basis of virtually all lookup actions within Mitopia®, and is the fundamental mechanism that underlies almost all Mitopia® cacheing schemes. The speed comes from the fact that as each character drives the state to the next state in the diagram, it is effectively eliminating any consideration of all other paths that are not derived from the new state. This yields a ‘search’ performance for the lexical analyzer when used as a “lookup” that is proportional to log(s) · L which is extremely fast and allows this approach to be used for dictionaries containing millions of entries without any appreciable slow down. This aspect of Lex is unrelated to its use in parsing contexts, but is an extremely useful side effect of the approach taken. For the same reason, the execution time of the first (single transition) phase of the Lex algorithm when recognizing reserved words and other fixed language tokens is O( log(s) ) which compares very favorably with the typical O(s**3) performance of the DFA based approach.
Execution time for the second phase of the algorithm is dependent on the number of range transitions described in the ordered list which is in turn determined largely by the number of variable sized tokens in the language. In almost all mining scripts developed so far, there are generally no more than 4 variable token types resulting in at most 20 range statements and a total of 15 distinct states. For a full blown programming type language such as Carmot-D (or E), the number of variable token types may rise to around 12 or 13, resulting in perhaps 60 range transition entries, but no more than 25 distinct states. Execution time of the second phase is therefore essentially independent of the number of states in the full state machine diagram, and is instead somewhat better than O(t) · L where t is the number of variable shaped token types. Once again this is a dramatic improvement over typical DFA based approaches.
The overall execution time for the algorithm depends on the relative frequency of reserved words to identifiers, but regardless of the balance, is almost as good as the best hand coded lexical analyzers, while preserving the benefits of auto-generated tables and a single universal algorithm requiring no custom code to be compiled.
Classic use of the Mitopia® Lexical Analyzer Package
Full details of the Mitopia® Lex two-phase algorithm are beyond the scope of this blog, however we can illustrate the benefits with a couple of examples. For our first example, we will look at the specification of a ‘word scanner’ for Arabic UTF-8 text. This application emphasizes the ‘range transition’ phase of the two phase algorithm over the single transition phase. The single and range transition specifications for the word scanner are shown in Listing 1 and 2 below:
 |
| Listing 1 – Mitopia® Lex Single Transition Specification for a UTF-8 Arabic word scanner |
 |
| Listing 2 – Mitopia® Lex Range Transition Specification for a UTF-8 Arabic word scanner |
When combined together into a functional lexical analyzer to implement the word scanner, the transition diagram resulting from the specifications above is as shown in Figure 3 below:
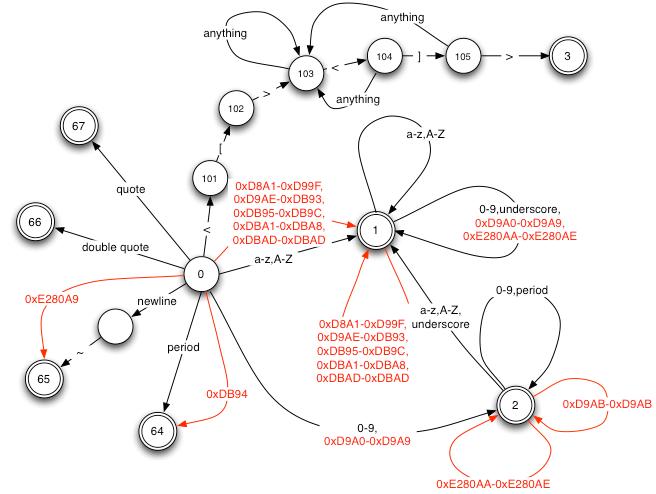 |
|
Figure 3 – Arabic Word Scanner State Transition Diagram
|
Note that there are just 13 distinct states in both diagrams combined which translates to incredibly rapid execution, and extremely small generated table size (just a few hundred bytes). Imagine how many states would exist in the DFA using the classical approach. Also notice that the analyzer is handling mixed and variable byte width characters, a thing unthinkable with standard approaches. Remember that the textual specifications shown above are dynamically converted to a lexical analyzer table which drives the algorithm, there is no compiled code output by the lexical analyzer generator, indeed the generator is immediately available for use after a single API call to create the tables. The speed with which this happens allows lexical analyzers to be created (and disposed) dynamically as part of low level highly performance sensitive code. Once again this would not be possible with classical approaches involving NFA/DFA conversion.
Dynamic Modification of Recognizers
The previous example showed how to create a lexical analyzer for a static language, i.e., one that does not change during the life of the lexical analyzer itself. Mitopia uses this approach pervasively to create languages that are custom tailored to the specific problem, or source to be parsed. This is where classical lexical analysis theory ends, the concept of a dynamically changeable lexical analyzer does not exist in classical lexical analysis. However, in Mitopia® it is just as common for lexical analyzers to be used in dynamic situations as it is in static situations, indeed this capability forms the underpinnings of much of what Mitopia® does.
In a dynamic situation, the language recognized by the lexical analyzer changes dynamically as new tokens are added to (and/or deleted from) the recognizer during a run. If one uses a classical approach to creating a lexical analyzer table, dynamic modification of the language is effectively impossible, however, by using Mitopia’s patented two table approach, it becomes possible to efficiently modify the single transition ‘OneCat’ table during a run to recognize new tokens. The lexical analyzer when used in this way becomes the basic building block of ‘content addressable memory’, that is it can be used to store and retrieve information about things simply by using the ‘name’ of the thing to locate the information involved. This is somewhat like looking things up using a hashing technique except that the lexical approach brings numerous benefits which we will describe later.
In fact, when creating a lexical analyzer ‘OneCat’ table for a static language (as described in the previous section), the actual table creation occurs as a series of calls to LX_Add() for each single transition token listed in the specification. It is also possible to call LX_Add() on an already created and running lexical analyzer table in order to add new tokens to the language dynamically. Figure 4 below illustrates the actual changes to an initially empty ‘OneCat’ table as a series of tokens are added dynamically.
 ‘OneCat’ table can be taken advantage of to alphabetize recognized tokens, and is also the key to the efficiency of LX_Lex() when used for lookup purposes.
‘OneCat’ table can be taken advantage of to alphabetize recognized tokens, and is also the key to the efficiency of LX_Lex() when used for lookup purposes.
Note the following about the sequence shown in Fig 4:
- All jump offsets are positive.
- The entries in the table are not stored in alphabetical order but instead in order of when they were added.
- As the table gets larger, the memory usage gets more efficient as more of the pre-existing strings are leveraged when adding new token strings.
- The logic used to add new entries is clear in most cases. Step 6 where the token “camels” when added causes an exception. In this case the token “camel” already existed and so the ‘offset’ field of the ‘OneCat’ that followed the ‘l’ contained the token number 3 for “camel” and is thus not available to hold the jump offset to the next alternative as in all prior cases. The logic is thus forced to insert a ‘null jump’ in place of the token number 3. A ‘null jump’ is an ‘OneCat’ record containing the illegal UTF-8 code 0xFF (i.e., ~0) in the ‘catalyst’ field together with a jump ‘offset’ to the next alternative record. In this case the trailing ‘s’ of “camels”. The ‘s’ entry also has a jump offset to the record corresponding to the original shorter token “camel” which has ‘0’ as the ‘catalyst’ character, indicating that no further input is required for acceptance.
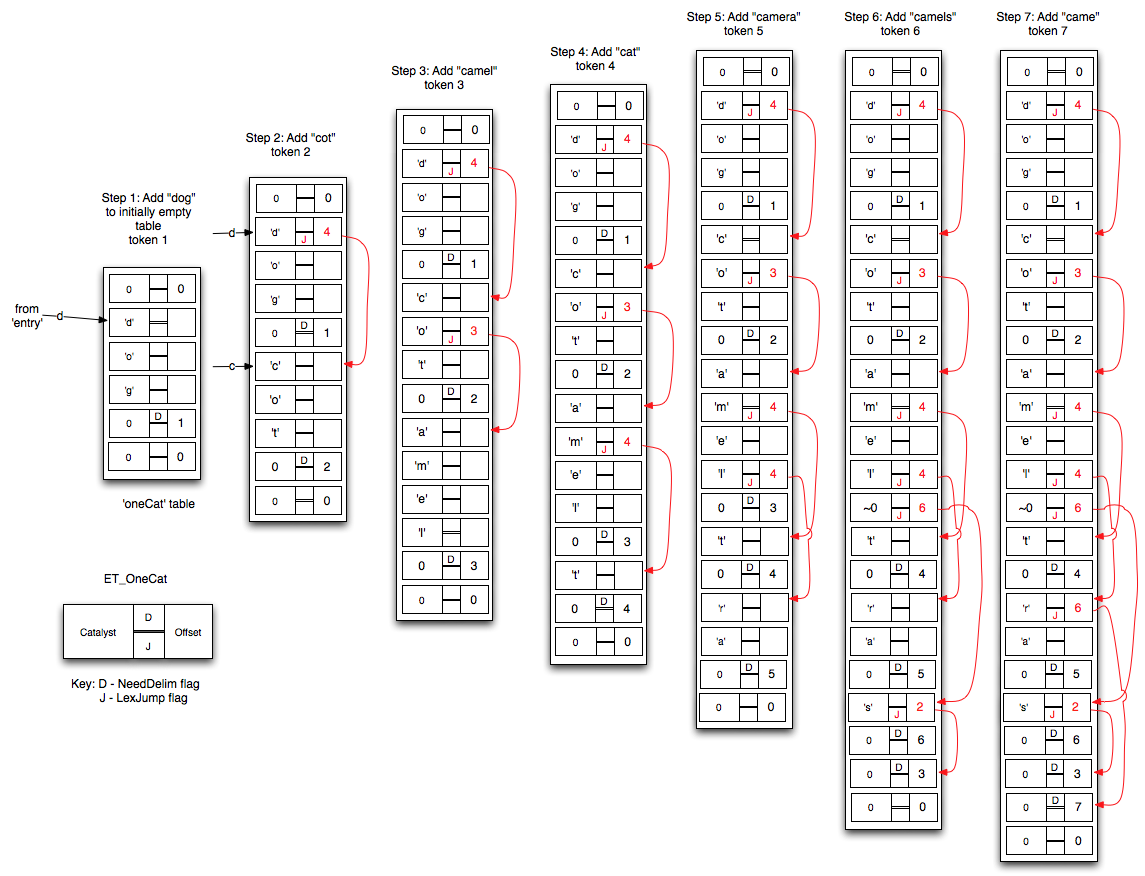 |
|
Figure 4 – Dynamically Adding Tokens to a Recognizer (Click to Enlarge)
|
It should be obvious from studying Figure 4 that is is possible to add new tokens to the existing lexical analyzer recognizer in a very efficient manner and without impacting recognition of the existing tokens defined for the recognizer. As mentioned above, the function used to do this is LX_Add(). This feature is key to the use of the lexical analyzer in dynamic situations and for such things as fast content addressable lookup. The tradeoff of course is that given the method used to add, it becomes much more difficult to remove items dynamically from the recognizer efficiently, indeed full removal essentially requires that the entire recognizer be listed and reconstructed from scratch which could be very slow for a large recognizer. The function LX_Sub() is used to remove items from an existing recognizer and thus can be slow for a large recognizer. Fortunately there is a very simple way to avoid this asymmetry but using the function LX_Set() to set the token value for an existing token to zero, thereby effectively removing it as far as future calls to LX_Lex() are concerned even though the entire definition of the token remains in the table after a call to LX_Set(). Unlike LX_Sub(), LX_Set() is a very efficient and fast function. The code snippet in Listing 3 below illustrates this for typical dictionary lookup access functions.
 |
|
Listing 3 – Generic Dictionary/Content Addressable Memory Lookup using Lex
|
How Fast is it?
One way to measure speed objectively is to compare with well known sorting algorithms such as QuickSort whose performance and speed as they scale have been extensively studied and documented.
One of the key advantages of the Mitopia® approach to lexical analyzer tables is the ease with which the entire content of the recognizer can be listed out in alphabetized order. This ‘sorting’ behavior that is inherent to the listing process is taken advantage of in a number of applications, including the explicit use of the lexical analyzer approach for very high performance sorting applications. To get some idea of the performance advantages for very large sorting applications, we can compare the performance of identical sorts using a highly optimized version of the QuickSort algorithm (the gold standard of for classical sort algorithms) versus the use of the lexical analyzer API. This test is actually part of the module test for Mitopia’s Sorting package since the range sort is used extensively within Mitopia servers in order to keep track of all ranges within a collection or other ‘flat’ aggregate that have been changed in order to minimize file I/O time. The ‘range’ sort/merge is implemented internally both ways in order to allow tradeoffs to be made between the two approaches. Here are representative results of a run of this test program (all compiler optimizations turned off):
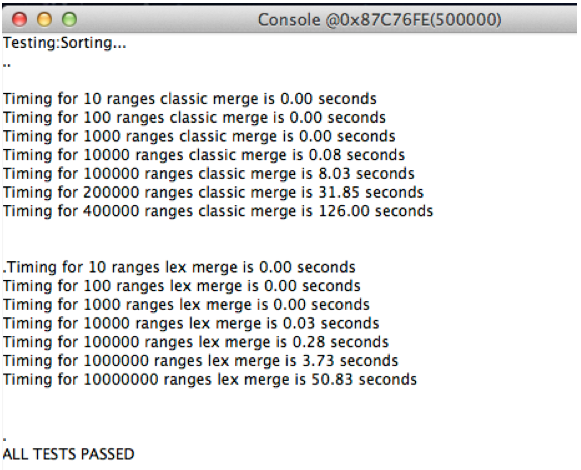 |
| Figure 5 – Performance of Lex when used for sorting |
Results show that the QuickSort algorithm starts to exhibit a serious performance bottleneck above 100,000 ranges being merged, such that execution time increases fourfold while the number of ranges doubles from 200K to 400K, that is the timing is proportional to N*log(N).
In stark contrast, the lexical approach takes less time to sort 10 million ranges than QuickSort does for just 400K and does not exhibit the same log(N) multiplier effect; that is even up to 10 million rages, as the number of ranges is increased by a factor of 10, the timing to sort them also increases by just marginally over a factor of 10. The timing is proportional to something slightly greater than N, and substantially less than N*log(N).
This kind of performance places the lexical sort out front of todays standard sort algorithms like QuickSort, and into the ‘radix sorting’ class. Like all sorting methods that fall into the general category of ‘radix sorting’, for the lexical sort, the price is the creation of an auxiliary structure or tree into which the items being sorted are arranged. In effect, the lexical analyzer OneCat table is such an auxiliary sorting structure, but unlike normal sorting algorithms, it is created not as part of any sorting process, but simply by virtue of creating the lexical analyzer table in the first place. Effectively, the process of adding symbols to a lexical analyzer simultaneously performs an extremely efficient ‘radix’ type sort, thus allowing the use of the lexical analyzer API for alphabetizing, sorting and listing tasks without any sort overhead for these features. This means that we can effectively take advantage of this dualism to get lexical sorting (i.e., symbol table listing) for free in many applications that might not be classically though of as ‘sorting’ situations. In addition for truly massive sorting and lookup tasks, we can use the lexical analyzer in preference to any classical technique in order to get the straight sorting performance boost we require. Perhaps just as importantly, sorting capabilities are inherently hierarchical, that is a lexical DB could for example represent the entire contents of a disk and all folders and files within it, and so provide in one form a rapid navigation, file lookup, and zero-overhead sort capability. The possibilities here are endless.
Another way to get an idea of the speed of the Lex algorithm is to look at the rate it is able to scan through a large text file when being used in a more classical parsing application such as the Arabic word scanner example above. The scanner listed will scan through and tokenize a large corpus containing UTF-8 Arabic text (52.5 million words) at an average rate of 8.3 MB/s (or 872,500 words/s) on a single core 3 GHz machine (2006 era). Simpler English/ASCII scanners run much faster.
Alternatively, we can ask how long does it take for LX_LEX() to re-scan and look up the same series of 52.5 million words from corresponding set of 773 thousand unique words (i.e., a Content Addressable Memory application – using ‘OneCat’ table primarily). On the same machine, the recognizer was able to look up words at a rate of 236,174 words/s (2.2 MB/s). Once again simpler English/ASCII scanners run at a much faster word rate.Finally of course the performances above are for the C software implementation of the algorithm. As mentioned in the “
A Stacked Deck” post, the LX_Lex() algorithm was designed from the outset to be implemented in either software (US 7,328,430) or hardware (US 8,099,722). The hardware implementation handles applications where scanning performance many orders of magnitude greater than those above are required, while still maintaining all the flexibility and adaptiveness of the approach. Again and again when we have encountered performance problems within Mitopia® that brought things to a standstill, particularly in server operations, queries, and caching applications, the solution has been to re-factor the code to take advantage of the Lex technology. Performance improvements of 2 or 3 orders of magnitude, consistently result.The Lex technology underlies virtually every high performance aspect of the Mitopia® architecture, as well as enabling the real-time creation of custom languages to handle any and all forms of interfacing and abstraction. Without it, it is hard to imagine creating an end-to-end Knowledge level platform such as Mitopia®.

 It turns out that the single most fundamental and pervasive operation for a Knowledge Level (KL) system is lookup by name or other identifying tag string. In a general sense this requires “Content Addressable Memory” (CAM). Because the CAM lookup operation is so pervasive in KL systems, often accounting for well over 50% of CPU time in common operations, an extremely fast algorithm or preferably a hardware implementation is required. Unfortunately standard CPUs provide no hardware support for CAM, which means a software algorithm must serve. Current approaches use hashing schemes, but these generally provide no means to get ‘close’, say if a name is slightly misspelt. Nor do hashes generally help with ‘paths’ and hierarchies which are fundamental to organizing ontological/KL data. If the hash lookup fails, you are essentially back where you started. Finding a solution to this problem is a key first step in implementing a KL system.
It turns out that the single most fundamental and pervasive operation for a Knowledge Level (KL) system is lookup by name or other identifying tag string. In a general sense this requires “Content Addressable Memory” (CAM). Because the CAM lookup operation is so pervasive in KL systems, often accounting for well over 50% of CPU time in common operations, an extremely fast algorithm or preferably a hardware implementation is required. Unfortunately standard CPUs provide no hardware support for CAM, which means a software algorithm must serve. Current approaches use hashing schemes, but these generally provide no means to get ‘close’, say if a name is slightly misspelt. Nor do hashes generally help with ‘paths’ and hierarchies which are fundamental to organizing ontological/KL data. If the hash lookup fails, you are essentially back where you started. Finding a solution to this problem is a key first step in implementing a KL system.




 ‘OneCat’ table can be taken advantage of to alphabetize recognized tokens, and is also the key to the efficiency of LX_Lex() when used for lookup purposes.
‘OneCat’ table can be taken advantage of to alphabetize recognized tokens, and is also the key to the efficiency of LX_Lex() when used for lookup purposes.



