Shortest path based universal stemming algorithm

In the previous two posts I have introduced both the concept of stemming as well as Mitopia’s framework for combining multiple stemming algorithms with backing dictionaries in order to improve stemmer accuracy in any given language. In this post I want to describe the basic concepts of the Fairweather Stemmer (referred to hereafter as the ‘new stemmer’), a patented new stemming algorithm that:

Can be applied to any language or scripting system held as UTF-8 text.
Can be trained by normal people to attain close to 100% accuracy in a language (standard algorithms max out at 30% or less). A complete GUI environment for training (not detailed in this post) is provided.
Unlike today’s algorithms, can generate multiple roots for any given word. Handles multi-root words, suffix and prefix stripping & mapping.
Generates true linguistic (human readable) roots.
Maps/conflates non-English stemmed roots to English equivalents to allow accurate cross-language and multi-language search.
Is fast enough to be applied in all standard stemming applications.
Runs within the previously described stemming framework and so can take advantage of high speed specialized dictionaries (people, places, proper names, acronyms, etc.).

Essentially this universal stemming approach, based as it is on shortest path techniques, rather than linguistic principles (which of course are different for each language), has the potential to replace all other stemming algorithms while vastly improving stemming accuracy and utility thus greatly improving text search, regardless of language. The technique is fundamental to Mitopia’s cross language querying capabilities, but can be applied in any other search context through use of the available stand-alone library.

Overview

Now that we have described the stemming framework itself and how it is integrated with any existing database, it is possible to describe the shortest-path based stemming algorithm in isolation from any surrounding context. As discussed previously, the new stemmer algorithm is based on the premise that in essentially all languages, it is possible to construct all word variations from the following basic pattern:

[ Prefix ] Root { [ Infix ] Root } [ Suffix ]

The algorithm requires an extremely fast lexical analyzer lookup in order to allow it to recognize all the various word portions above. In the preceding description of the basic stemmer context structure, the fields ‘fRoots’, ‘fPrefix’, ‘fSuffix’, and ‘fInfix’ represent the various recognizers required by the lexical analyzer LX_Lex() in order to recognize all allowed string fragments that make up any of the legal values for the root, prefix, suffix, and infix sequences in the language concerned. These dictionaries are loaded automatically during initialization (within “makeStemmerContext”) by the framework if the corresponding files are present in the directory for the language concerned. Given these dictionaries, the algorithm for the stemmer comprises a main routine and a recursive subroutine, where the main routine essentially handles exploring all possible combinations of prefix and suffix (including of course no prefix and no suffix), while the recursive inner subroutine is responsible for exploring all sequences of root(s) and infix fragments that could make up the central portion of the word being stemmed. The inner subroutine must be recursive (or equivalent) in order to handle arbitrary numbers of roots within a word as implied by the phrase “Root { [ Infix ] Root }”.

If there is more than one prefix or suffix involved, the algorithm sorts them by increasing order and then appends the no prefix and no suffix case to the end of this sorted list. The prefix/suffix loop in the main routine then start from the no prefix/suffix case and proceed backwards from the longest prefix/suffix to shorter prefixes and suffixes. This strange ordering is chosen for a number of important reasons viz:

By starting with the no prefix, no suffix case, the common case of recognizing a word that is already a complete root word (i.e., has no prefix or suffix) is examined first, and if found, the loops are immediately terminated thus ensuring that this common case results in minimal execution time.
Sometimes as a result of the vagaries of the cost curves discussed below, a situation arises where the minimum cost path through a word does not result in the correct stem, and this cannot be fixed by any other means that adding a longer root word fragment mapped to the same root output to cause a new lower cost path. The fact that the no affix (i.e., no suffix and prefix) case occurs first allows this technique to be used in the final resort to solve any otherwise unsolvable problem with cost calculations, since as can be seen, the routine will stop immediately if it recognizes a naked root word.
After the no suffix/prefix case, the fact that the loop then continues in decreasing order of affix size is taken advantage of by the inner recursive function in order to differentially favor longer trailing roots in the word over longer suffixes, and this logic significantly reduces the amount of dictionary tweaking necessary to overcome suffix/trailing root ambiguities.

When constructing the list of suffixes for any given word, the function first inverts the order of the characters in the word, and then uses a variant of LX_Lex() to obtain a set of suffixes. It was noted earlier that the custom option ‘kFlipCharOrder’ when passed to the dictionary load routine, causes it to construct a recognizer for the dictionary entries with the character order swapped. Since this option is always specified when suffix dictionaries are loaded, the recognizer is already set up to recognize the suffixes that start the flipped word to be stemmed, and thus the algorithm avoids a great deal of time and complexity that would otherwise be required in order to obtain a list of all potential suffixes.

Cost Calculations

The algorithm obtains a cost measure for both the prefix and suffix as well as roots and infixes by calling the cost calculator function set up in the basic context field ‘fCostCalc’, and passing it the word part involved, the number of characters involved, and the average number of bytes per character for the language (set up by the “makeStemmerContext” call in the basic context field ‘bytesPerChar’ which is 1 by default). It is actually possible to alter this calculation for a given language by overwriting the default value placed in this field by QX_InitBasicStemContext(). Thus far however, and somewhat surprisingly, we have found that the default cost calculator function appears to work well for all languages, regardless of script system, and for this reason, it it recommended that you do not change the cost computation for your language unless it is clear that some unique feature of the language makes this necessary.

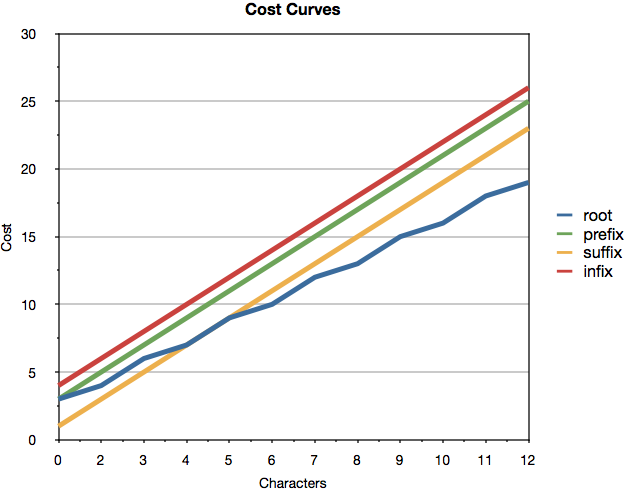If we plot the cost curve for each word part against the normalized number of characters involved (i.e., divided by the average number of UTF-8 bytes per character in the language) we see the graph depicted above.

root: cost = 2N – N/2 + 1
prefix: cost = 2N + 1
suffix: cost = 2N -2
infix: cost = 2N + 2

From the cost curves we can see a number of significant points that are crucial in order to minimize the number of special cases that must be explicitly handled in the dictionaries, thereby minimizing dictionary size and reducing the amount of work necessary to get correct results in all cases.

The first point is that at the low end of the character axis, the cost of suffixes is significantly less than that of roots, whereas as the root fragments become longer they become significantly cheaper than the corresponding suffix. This behavior serves two main purposes, the first is that the algorithm tends to favor small suffixes at the end of a word rather than finding a path by stringing together multiple roots. As an example, consider the English word “contraction” which can be parsed either as two roots as in “contract” and “ion” for a cost of 20, or as a single root “contract” followed by the suffix “ion” for a cost of 17. This behavior causes the ambiguity between small trailing root words like “ion” and suffixes to be resolved in favor of the suffix in most cases, and it turns out that this is normally the appropriate behavior. As the length of the suffix increases however, this behavior becomes inappropriate, since long suffixes might cause significant trailing roots to be lost. An example of this is the English word “rationalistically”, which can be parsed in two ways, namely as the root “ration” followed by the suffix “alistically” (cost 30), or the root “rational” followed by the suffix “istically” (cost 29). The increased cost associated with the long suffix “alistically” is what causes the longer root “rational” to be chosen over the shorter root “ration”. We can see that there is a grey area in the curves for root and suffix sizes of 4 or 5 characters, and it is this grey area that is the reason why the algorithm proceeds from the longest suffix to the shortest, since this allows the inner recursive loop to detect a situation where the costs are identical and choose in favor of the longer root when this occurs. Because the longer root will be examined after the shorter one, the algorithm has all the information necessary to make the right choice.

The higher costs of prefix fragments over roots ensures that prefix sequences are only chosen over alternate root fragments when appropriate, and the various words beginning with “ab” in Table 1 show examples of this behavior. The fact that infix sequences are far more expensive than any other component is designed to prevent the possibility of multi-root words being chosen over longer roots as a result of being split by small one or two letter infix sequences.

The plus 1 term for root words is critical in ensuring that any word that can be interpreted either as two adjacent roots or as a single longer root is resolved in favor of the longer root. An example in English might be the word “beestings” which has nothing to do with bees or their stings. In addition, the inner recursive routine keeps track of its recursion depth which corresponds to the number of roots that have been chained together in the path, and it also adds this depth value to the cost for any root word fragments. This results in paths constructed by chaining multiple small roots becoming progressively more expensive as the number of roots increases. This again has the beneficial effect of further favoring longer roots. As mentioned above, experience has shown that these curves appear to work quite well regardless of language, however, the framework allows alternate cost curves to be substituted for any language if the defaults do not result in easy dictionary management.

Mapping Fragments to Stemmed Output

Another aspect of the outer stemming algorithm that still needs to be explained is it’s behavior in copying the results of the stemming process back to the stemmed output buffer. The inner recursive algorithm, which evaluates root and infix sequences, returns the result of the inner parse into a buffer (which may contain one or more words as a result of root word mapping) to the outer routine. Since both prefix and suffix fragments can optionally be mapped to an output word, the outer routine must assemble a sequence of words in the right order to represent the extracted meaning. This behavior of outputting multiple words in response to stemming is unique to the new stemmer and yet it is critical to improving search results since without it, prefix stripping (at least in English) becomes impossible, and the dictionaries must be much larger and also less expressive. Examples of the need for this are shown in Figure 1 (earlier post) where the words “abnormally” and “abaxial” are broken into two output words with a leading “not” that is generated as a result of prefix mapping. In English, if the stemmer failed to do this, and the search was for the word “normal”, then no hits would be returned for documents containing the word “abnormal”, even though this is incorrect behavior. Note however that with the new stemmer this is not the case. Also note that searches for “abnormal” will return not only hits containing words derived from “abnormal”, but more importantly, if the author chose to say “not normal” instead of “abnormal”, these documents will also be returned as a result of stemming on the query terms.

The mapped fragments for the prefix and suffix, if relevant (suffixes in English rarely result in a mapping, whereas prefixes usually do, but the situation is different in other languages), are fetched from the appropriate dictionaries and pre-pended by default to the output text. Note however that the algorithm allows the dictionary entry to start with a “+” character, and this instead results in appending the word after the word(s) resulting from root mapping. In other languages, due to the differing ordering or words, it is often more correct to append rather than prepend affix mappings, and clearly this is fully supported by the algorithm. The multi-root words in Table 1 such as “abdominothoracic” and “abdominoanterior” are also examples of how existing stemming approaches fail to provide accurate search results, since if the search was on the word “abdomen”, neither of these words would result in hits in a classic stemming system. Similarly a search on “thorax” would fail to return documents containing the word “abdominothoracic”. In certain specialized fields such as medicine or chemistry, where words are commonly constructed from multiple significant roots (the word divinylbenzene in Table 2 is an example), this shortcoming in today’s text search systems can be critical, and hence the new stemming algorithm can provide considerable benefit.

One complexity that has been glossed over up until now is the fact that certain prefix and suffix fragments may well be identical to a root fragment (examples are the prefix “arch” or the suffix “less”). In these cases the algorithm will probably choose the root over the affix because of the cost curves, whereas we may instead wish to re-interpret (or suppress) the meaning if the root is being used as an affix rather than a root. For example in the English word “clueless” we may wish to map the trailing root “less” in this case to cause the stemmed output to become “without clue” which is the correct effect of the suffix “less”. Clearly we cannot do this if the “less” is recognized as a root since its meaning as a root is simply “less”. In fact the situation can be considerably more complex, an example being the trailing suffix/root “able”, “ably”, “ability”, “abilities”, “ableness” etc. If we wish to recognize these words as suffixes and strip them off to produce no output (i.e., “teachable” -> “teach” and not “teach” “able”), we must make sure that for the root “able”, all possible suffix forms are recognized by the root dictionary, and then in the suffix dictionary we must also enter each suffix form of “able” and map the output to “-” alone. A mapped output starting with a ‘-’ character forces the affix to be output before the root words, but this is redundant since this is the default behavior, and so a mapping of just “-” with no additional text can be used to suppress output altogether. Similar cases occur with roots used as prefixes so for example when the root “arch” occurs as a prefix (as in archangel), its meaning on output must be re-mapped to “chief” rather than “arch”. The logic associated with detecting and performing these essential re-mapping behaviors is quite complex and is invoked within the algorithm as required. Without these behaviors, certain words in many languages cannot be stemmed to their true meanings.

Some of the same problems occur with certain root fragments independent of affixes. For example, consider the English word “sexennial” which may be recognized as a fragment leading to recognizing the root word “six” but the remaining “ennial” cannot realistically be associated with the word year since the spelling in this case is not derived from “annual”. In this case we want to preserve the hidden root “ennial” as “year” in our output as in “six year”. To do this we can enter the fragment itself under the root “six” using the form “sexennial+year” and as in other occurrences of the ‘+’ character is dictionaries, this causes the text that follows the ‘+’ to be output after the root. In fact in other languages, the situation can be more complex than this and the root dictionary fragments support any of the following forms:

fragment — simply copy the corresponding root word to the output buffer
fragment- — this means the root cannot be followed by other roots. Handy for dealing with overlapping situations such as “super” and “superb” as in the word “superbitch” in order to force “super bitch” rather than “superb itch”.
fragment-root2{ root2n} — copy root2 (and optionally any following roots) to output buffer, followed by space, followed by root word
fragment+root3{ root3n} — copy the corresponding root word followed by a space, then root3 (and any following roots) to the output
fragment-root2{ root2n}+root3{ root3n} — effectively the same as adding the two preceding forms allowing output both before and after the root

Once again, the logic to handle these output mappings is complex and in broken out into a separate routine invoked by the main stemmer routines. The dictionary option “kStopAtPlusMinus” discussed under the “makeStemmerContext” plug-in is required in order to support this behavior and by default is set for the “fRoots” dictionary.

In this post we are only interested in describing the behavior of the algorithm at a sufficient level to allow understanding for the purposes of populating the stemmer dictionaries and resolving conflicts in the cost calculations when they occur.

The top listing (1) above gives the high level pseudo-code for the outer function of the algorithm, while lower listing (2) gives the pseudo-code for the inner recursive function. For clarity, most of the details have been omitted from both listings. The routine of (2) has two sections, the upper section handles recursive calls looking for the sequence “{[ infix ] Root }” while the lower section handles the initial “Root” term which cannot be preceded by an infix sequence. Obtaining a list of all possible infix sequences in handled in the same manner as obtaining a list of affixes in the outer algorithm, but uses the ‘fInfix’ dictionary and given this list, the routine loops over all possible infixes, computing the infix cost and then calling a variant of LX_Lex() to recognize any trailing root. If a trailing root is found there are two possible conditions, either that root contains enough characters to complete the path, or it does not, in which case the routine must call itself recursively to look for another “[infix] Root” path to complete the parse of the remaining characters.

As with the outer routine, the infix and root costs are compared with the minimum cost found so far in order to determine if a new lower cost path through the inner text has been found, and if so, the mapped output for this path is copied to the output buffer. Note that the routine adds the recursion depth ‘depth’ to the cost for any root found, and, as discussed previously, this logic is intended to favor finding longer roots over sequences of smaller roots. In the case where the current root is the last root required to complete the parse, the routine contains logic to determine if this root is longer than any previously found trailing root, and if so, to alter the root cost in order to cause the resulting path to be 1 cheaper than the previous path with the shorter trailing root. As discussed previously, this logic is intended to favor longer trailing roots over longer suffixes.

The actual code for these routines is considerably more complex, and is heavily instrumented to allow callers to obtain a detailed insight into the paths explored by the algorithm and the cost calculations involved. This fact is taken advantage of extensively by the development GUI to allow the dictionary developer to understand how the algorithm is operating in any given stemming sequence.

Stemming Compound Words, an Example

To give an example of the true power of the algorithm to take apart complex words, consider the English word “abetalipoproteinemia” which is a rare disorder affecting the absorption of fats and vitamins. The disease is related to the affliction “lipoproteinemia”, which is in turn derived from the root words “lipid”, “protein”, and “emia” meaning disease or sickness. The “abeta” portion of the word refers to a special group of lipids known as “beta” lipids and the preceding “a” implies that the root of the disorder is the inability to transport beta lipids. Obviously any conventional stemming algorithm has absolutely no chance of maintaining the relationships of this word with any of the constituent parts of the word after stemming, and thus anyone searching on any of these concepts will be unable to directly find any reference to this rare disorder.

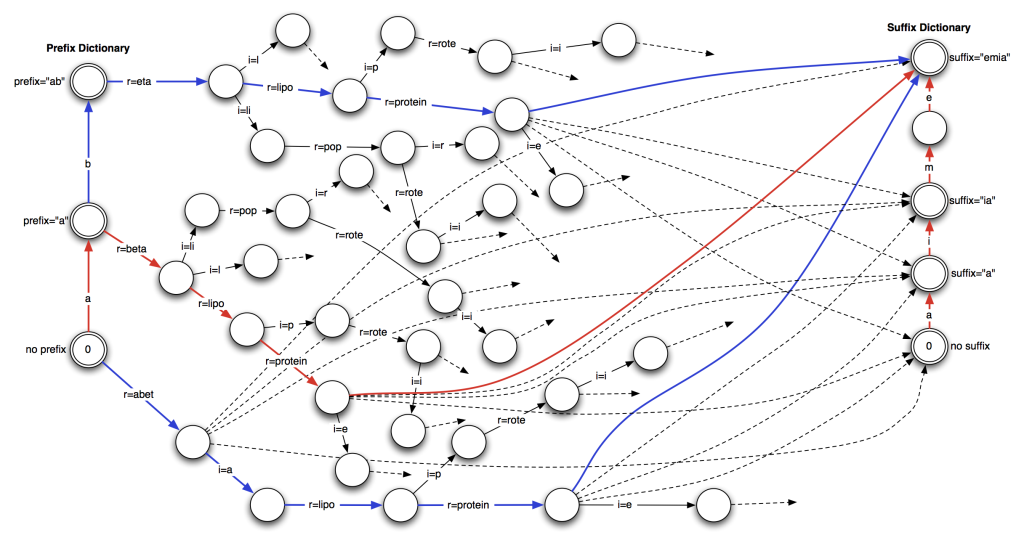
Figure 1- Stemming the Word “abetalipoproteinemia”

Figure 1 above shows the debugging printout from the Mitopia® stemming development environment when asked to stem the word “abetalipoproteinemia”. Each line of the printout represents a possible path to stemming the word explored by the algorithm. Notice first that the stemmer output is “not beta lipid protein sick” which amazingly enough, is exactly the output one would require in order to maintain searchability of this disease and all its related concepts. The format of the “Paths” listing in Figure 1 will be described in detail later, however, from the listing we can see that the algorithm explored a total of 81 possible paths through this word, finding just 3 complete paths to account for the entire word. Of the paths found, the lowest cost path (with a total cost of 38) was comprised of the following sequence of fragments:

Prefix:’a’, Root:’beta’, Root:’lipo’, Root:’protein’, Suffix:’emia’

After output mapping, this path results in the correct stemming output of “not beta lipid protein sick”. Clearly anyone searching on the terms “lipoproteinemia”, “proteinemia”, “lipid”, “protein”, “beta lipid” and any one of a number of other search terms, would have correctly found this reference giving this stemmer output, and such cannot be said of any other algorithm.

To clarify the path searching nature of this algorithm including the inner paths, Figure 2 below illustrates the complete set of paths explored by the algorithm for this one word as indicated by the path listing shown in Figure 1. In Figure 2, dotted paths indicate a failed attempt to connect the node to indicated suffix (an unconnected dotted path indicates failure to connect to all suffixes). The chosen path is indicated in red while the two alternate paths (more costly) are indicated in blue. The label “r=” indicates a fragment chosen from the “fRoots” root dictionary while “i=” indicates a fragment chosen from the “fInfix” infix dictionary.

Figure 2 – Paths Through the Word “abetalipoproteinemia” (Click to enlarge)

Understanding Stemmer Path Traces

The format of the shortest path search trace displayed in the paths display control is a series of one line entries comprised of the bracketed path segments that make up the path being explored as follows:

[P:prefix | cost] – This is the prefix sequence in effect for the path concerned and also the cost for that prefix according to the cost-calculator function. If there is no text between the ‘:’ and the following ‘|’, no prefix was in effect. In most cases is there is no prefix in effect, the “[P:…]” sequence is omitted entirely.
[S:suffix | cost] – This is the suffix sequence in effect for the path concerned and also the cost for that suffix according to the cost-calculator function. If there is no text between the ‘:’ and the following ‘|’, no suffix was in effect. In most cases is there is no suffix in effect, the “[S:…]” sequence is omitted entirely.
[I:infix | cost] – This is the infix sequence in effect for the path concerned and also the cost for that infix according to the cost-calculator function. If there is no text between the ‘:’ and the following ‘|’, no infix was in effect. In most cases is there is no infix in effect, the “[I:…]” sequence is omitted entirely.
[R:root | cost] – This is the root sequence in effect for the path concerned and also the cost for that root according to the cost-calculator function.

Since there can be multiple roots in sequence with optional infix fragments between them, multi-root words may display a repeated series of infix and root blocks on any given line. Figure 1 in the preceding section shows a good example of a large and complex path dump.

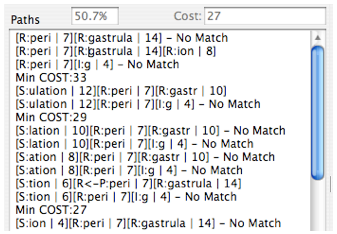
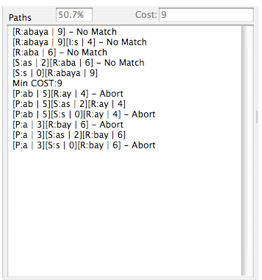The order of the lines appearing in the output correspond to the search order used by the algorithm to explore the paths. If a path fails to complete a successful parse, the corresponding line terminates with the text “– No Match”. If the algorithm determines that the cost of the path so far exceeds the current minimum cost, even if it has not completely explored the path, it aborts and the line is terminated with the text “– Abort” (see the screen shot to the right). This optimization behavior is not detailed in the description of the algorithm since it is not relevant to the algorithm itself but is merely a timing optimization. In addition, the algorithm contains a further optimization to not explore the recursive inner portion for the same prefix if on a previous pass, the total number of characters processed is less than that implied by the selected suffix length, since it is clear without exploration that this would not lead to a positive result. This optimization will cause the path line to be terminated by the string “– Not Tried”. This optimization can significantly improve execution time, but is not described in this document to avoid obscuring the basic algorithm.

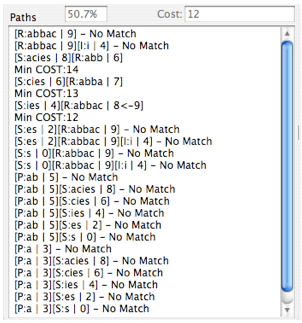Occasionally for the root word cost, the form “cost<-cost” may be displayed as in the screen shot to the right (for the word “abbacies”). This is an indication that the logic associated with favoring longer trailing roots has caused the root cost to be adjusted downward (from 9 to 8 in this case) in order to accomplish this feature. You may also see cost editing indications for affixes which are the result of other specialized logic to try to force correct operation without the need for word-specific adjustments in the largest number of cases.

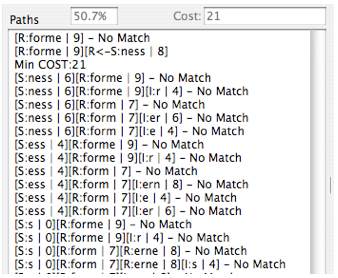
As previously discussed, it is quite often the case that an affix sequence is also a valid root word but when used as an affix, we want it to output a different meaning (or possibly to suppress the root output entirely). You will see cases in the paths listing where the techniques described to re-map affix outputs to change or suppress the root shown as entries of the form “[R<-P:cost]” or “[R<-S:cost]” depending on if a prefix or suffix is involved. The screen shots above for the words “perigastrulation” and “formerness” illustrate the appearance of these features.

In the prefix example, the word “peri” exists in both the root word and the prefix dictionaries but it is mapped to the root word “around” in the prefix dictionary. When “peri” is used as a prefix as part of a shortest path, the fact that it has a mapping to the root “around” is discovered and the form “R<-P” indicates that this mapping has been made by the algorithm (with a corresponding cost reduction from 9 for the prefix “peri” to 7 for the root “peri”). In the “formerness” case, the word “ness” is both a suffix (in which case it should be suppressed entirely i.e., mapped to “-”) and a root. In this case the recognition of the suffix “ness” as part of a shortest path results in mapping to the root form “ness” which is suppressed on output by the “-”. This mapping actually results in a cost increase from 6 for the suffix to 8 for the root form. The use of these techniques to resolve stemming conflicts between affixes and roots is discussed later. Be aware that the lines beginning with “Min COST:” in the listing indicate that one of the preceding lines contains a minimum cost path though not necessarily the immediately preceding line. This delay in printing the minimum cost indication is caused by the recursive nature of the algorithm and it means that you may have to scan upwards in the listing to find the line that corresponds to the cost indicated. Possible candidate lines will always end without a trailing text sequence such as “– No Match”.

The use of the root fragment mapping form “fragment-” (see earlier discussion) may result in output of a line ending in “– Inhibit” which implies that no further roots were examined because the earlier root fragment cannot be followed by other roots.

Because of the recursive nature of the stemming algorithm, the sequence in which the various affixes are tried determines the order in which the entries in the list are tried and printed out. As discussed earlier, the outer function of the algorithm first tries the case where there is no prefix, and within that case it then loops over the suffix cases starting with no suffix, then from the longest suffix down to the shortest. The outer function then proceeds to the longest available prefix and loops through all suffix forms as for the previous loop. This process is repeated until the possibilities for the shortest available prefix have been fully explored. Since this is the order the algorithm uses to explore the paths, this is also the order in which the path dump is listed. The prefix and suffix portions of the list for each line are always displayed before the results produced by the inner recursive function of the algorithm for the infix/root sequences.

The root listing will often contain lines that do not fit into the space available for the text control that contains the listing and these lines will be “wrapped” and continue onto the next line of the display. You can increase the horizontal size of the text control by growing the window and also by enlarging the lower panel area allocated to the paths listing by use of the panel resize control. See the GUI description for details.

Many of the lists displayed in auxiliary windows associated with the stemming development environment contain a list column entitled “Min Cost Path”. This column contains the one line from the full path listing (as described in this section), that was chosen as the final minimum cost path for the successful stemming operation. Understanding the contents of the cells in the “Min Cost Path” column is therefore just a subset of the problem of understanding the full path list described in this section.

Summary

As can be seen, in the case of this word, there are approximately 40 distinct ‘nodes’ in the diagram and the relationship between this algorithm’s approach to stemming words and the “traveling salesman” or shortest path problem is clear. Shortest path problems are normally very compute intensive, however in this case the combination of the fast lookup using Mitopia’s lexical analyzer together with taking advantage of the directed nature of the paths, allow the algorithm to be implemented with no significant increase in execution time over traditional stemmer algorithms.

The most important thing to remember about stemming is that its purpose is to improve the accuracy of text search, not to improve the readability of the output text (which may never be viewed). It is clear then that if the system is searched using the key word “abetalipoproteinemia”, it should return all instances of this word (and plurals etc.). You might think that since the word was broken up into the phrase “not beta lipid protein sick” as it was indexed into the database, that this would make it harder to find when the search term was “abetalipoproteinemia”. However, the search terms themselves must obviously be stemmed in an identical manner before they are checked against the database index, and so a one word search for the word “abetalipoproteinemia” is turned into a search for the sequence of words “not beta lipid protein sick” immediately next to each other, and hence correctly returns all matching words in the text database. This means that since this stemmer violates the almost universal assumption that the output of a stemming algorithm is just a single word, the database engine itself must be modified somewhat to be aware of the multi-word stemmer output, and to modify queries into sequence queries as necessary to account for it. Once this has been done, it is clear that we have a system that operates similarly in this simple case. Of course this is only the tip of the iceberg as far as search is concerned, since each stemmed word in the phrase “not beta lipid protein sick” has been separately indexed into the database and so it is possible to search on “lipoproteinemia” or just “proteinemia” and find hits for these diseases as well as “abetalipoproteinemia”. This is because a search for “lipoproteinemia” will be turned into a sequence search for “lipid protein sick” while a search for “proteinemia” will be a sequence search on “protein sick” and thus both key words will return hits for “abetalipoproteinemia” also. This is as it should be obviously, but no existing system is capable of this kind of search due to limitations in today’s stemming algorithms. Obviously, searches on “lipids”, “sicknesses” and a wide variety of other relevant terms will also correctly find references to this disease, which once again is a critical behavior for researchers in the medical field, and which is not possible with conventional search systems. More importantly, as we will see later, the goal is to facilitate search across all languages without regard to the query language. Compound words like this in any language will prevent and cross-language search for lack of a common root. The new stemmer algorithm overcomes this problem by allowing words in all languages to be broken into simple and mappable root word sequences and thus a multi-lingual search in Arabic using the Arabic word for sickness should correctly return a hit for “abetalipoproteinemia”!

Over and above the higher accuracy of the Fairweather stemmer (up to 100% vs 30%) in dealing with conflating word variants that may not follow the normal rules of the language (e.g., teach and taught) thereby improving search accuracy, it is the algorithm’s ability to maintain the important relationships within a word by converting complex words to word sequences, as illustrated above, that is its most important benefit, and which holds the potential to revolutionize text search as it exists today.